Solving a System of Differential Equations Containing a Diffusion Equation with Nonlinear Terms on the Example of Laser Heating in Silicon
Abstract
:1. Introduction
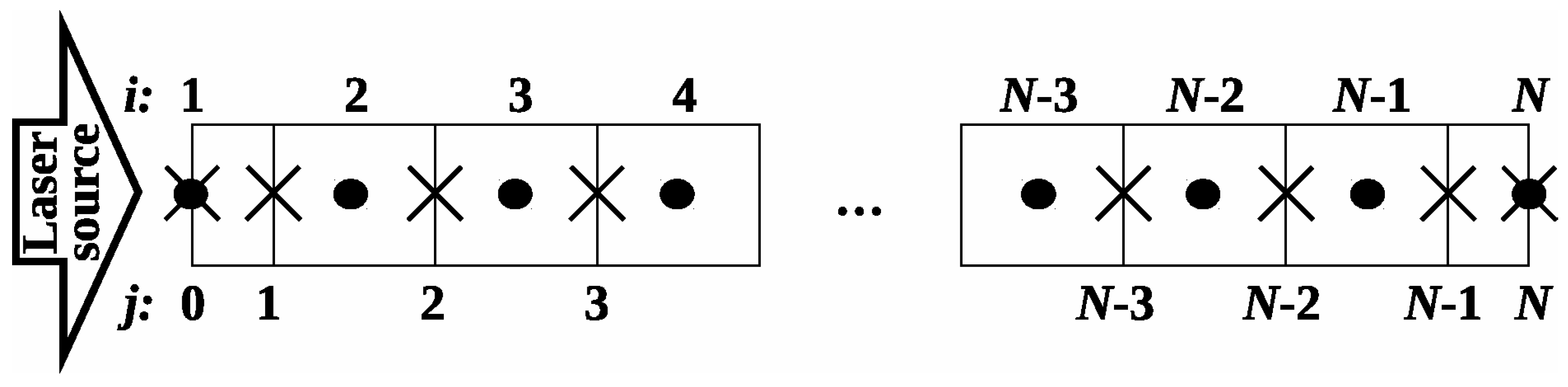
2. Model Description
3. Numerical Solution Scheme
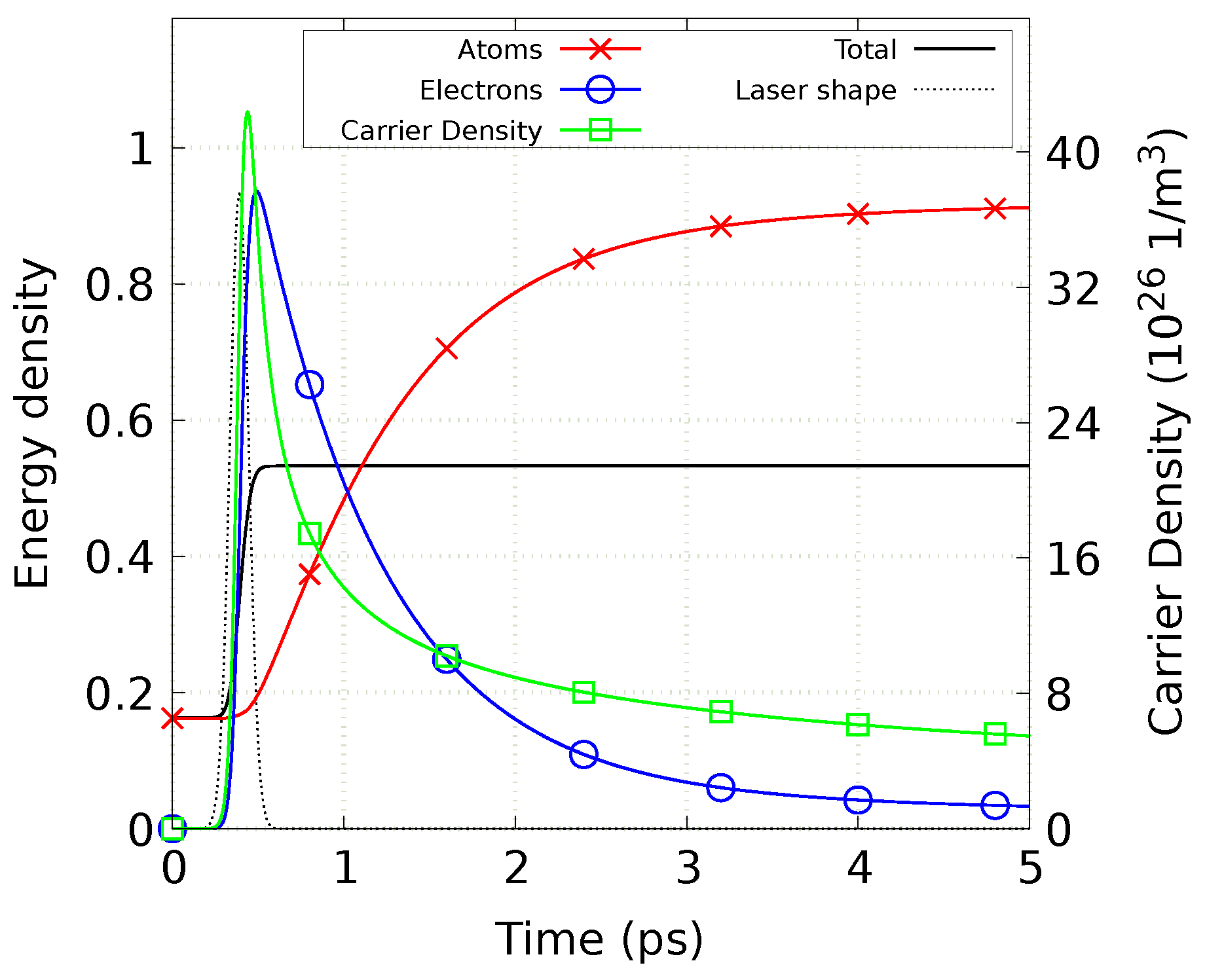
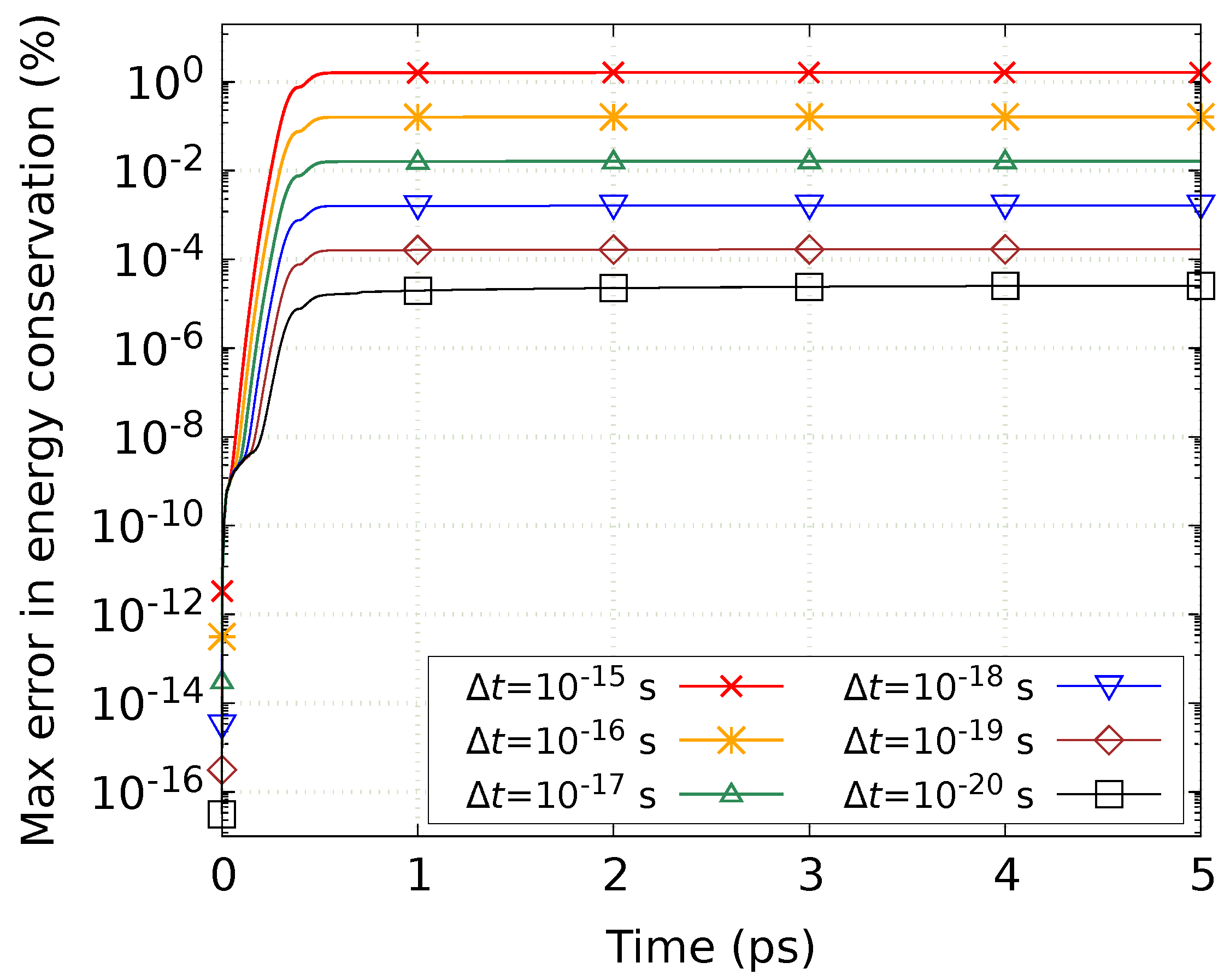
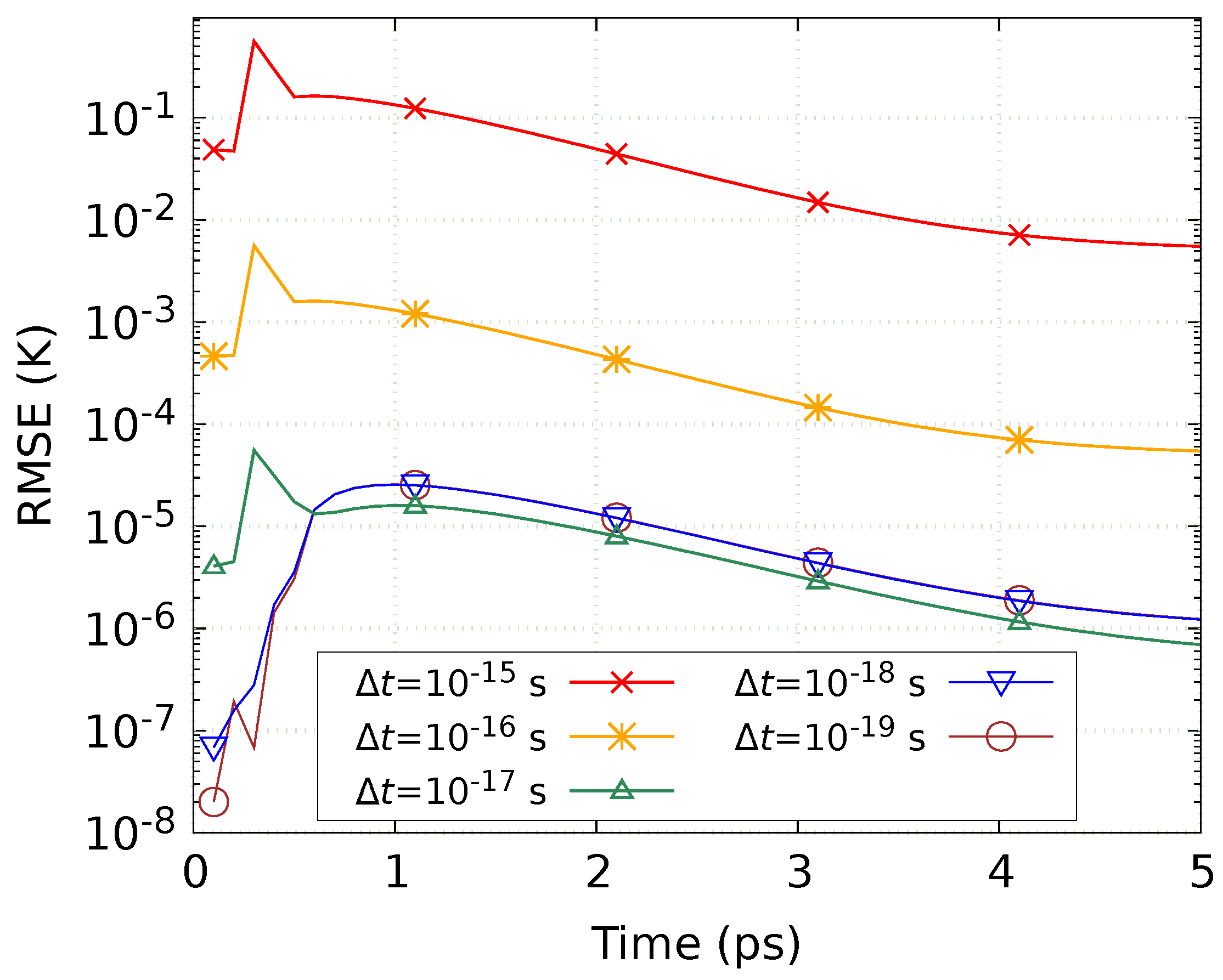
4. Calculation Example
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, Z.; Zhao, J.; Yin, J.; Li, H. Nonlinear Diffusion Equations; World Scientific: Singapore, 2001. [Google Scholar]
- McKane, A.; Waxman, D. Singular solutions of the diffusion equation of population genetics. J. Theor. Biol. 2007, 247, 849–858. [Google Scholar] [CrossRef] [Green Version]
- Bower, J.M.; Bolouri, H. Computational Modeling of Genetic and Biochemical Networks; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Aubert, G.; Kornprobst, P. Mathematical Problems in Image Processing: Partial Differential Equations and the Calculus of Variations; Springer Science & Business Media: New York, NY, USA, 2006; Volume 147. [Google Scholar]
- Nagasawa, M. Schrödinger Equations and Diffusion Theory; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Bäuerle, D.W. Laser Processing and Chemistry; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Liu, X.; Du, D.; Mourou, G. Laser ablation and micromachining with ultrashort laser pulses. Quantum Electron. IEEE J. 1997, 33, 1706–1716. [Google Scholar] [CrossRef]
- Chichkov, B.N.; Momma, C.; Nolte, S.; Von Alvensleben, F.; Tünnermann, A. Femtosecond, picosecond and nanosecond laser ablation of solids. Appl. Phys. A 1996, 63, 109–115. [Google Scholar] [CrossRef]
- Gattass, R.R.; Mazur, E. Femtosecond laser micromachining in transparent materials. Nat. Photonics 2008, 2, 219–225. [Google Scholar] [CrossRef]
- Chou, S.Y.; Keimel, C.; Gu, J. Ultrafast and direct imprint of nanostructures in silicon. Nature 2002, 417, 835–837. [Google Scholar] [CrossRef] [PubMed]
- Le Harzic, R.; Dörr, D.; Sauer, D.; Stracke, F.; Zimmermann, H. Generation of high spatial frequency ripples on silicon under ultrashort laser pulses irradiation. Appl. Phys. Lett. 2011, 98, 211905. [Google Scholar] [CrossRef]
- Huang, P.H.; Lai, H.Y. Nucleation and propagation of dislocations during nanopore lattice mending by laser annealing: Modified continuum-atomistic modeling. Phys. Rev. B 2008, 77, 125408. [Google Scholar] [CrossRef]
- Stratakis, E.; Ranella, A.; Fotakis, C. Biomimetic micro/nanostructured functional surfaces for microfluidic and tissue engineering applications. Biomicrofluidics 2011, 5, 013411. [Google Scholar] [CrossRef] [Green Version]
- Mathis, A.; Courvoisier, F.; Froehly, L.; Furfaro, L.; Jacquot, M.; Lacourt, P.A.; Dudley, J.M. Micromachining along a curve: Femtosecond laser micromachining of curved profiles in diamond and silicon using accelerating beams. Appl. Phys. Lett. 2012, 101, 071110. [Google Scholar] [CrossRef] [Green Version]
- Bhuyan, M.K.; Courvoisier, F.; Lacourt, P.A.; Jacquot, M.; Salut, R.; Furfaro, L.; Dudley, J.M. High aspect ratio nanochannel machining using single shot femtosecond Bessel beams. Appl. Phys. Lett. 2010, 97, 081102. [Google Scholar] [CrossRef]
- Anisimov, S.I.; Kapeliovich, B.L.; Perel’Man, T.L. Electron emission from metal surfaces exposed to ultrashort laser pulses. Zh. Eksp. Teor. Fiz 1974, 66, 375–377. [Google Scholar]
- Van Driel, H.M. Kinetics of high-density plasmas generated in Si by 1.06-and 0.53-mkm picosecond laser pulses. Phys. Rev. B 1987, 35, 8166. [Google Scholar] [CrossRef]
- Ivanov, D.S.; Zhigilei, L.V. Combined atomistic-continuum modeling of short-pulse laser melting and disintegration of metal films. Phys. Rev. B 2003, 68, 064114. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.K.; Tzou, D.Y.; Beraun, J.E. Numerical investigation of ultrashort laser damage in semiconductors. Int. J. Heat Mass Transf. 2005, 48, 501–509. [Google Scholar] [CrossRef]
- Isaacson, E.; Keller, H.B. Analysis of Numerical Methods; Dover Publications: New York, NY, USA, 2012. [Google Scholar]
- Crank, J.; Nicolson, P. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. Math. Proc. Camb. Philos. Soc. 1947, 43, 50–67. [Google Scholar] [CrossRef]
- Cebeci, T. Convective Heat Transfer; Springer: Berlin/Heidelberg, Germany, 2002; Volume 1. [Google Scholar]
- Ivanov, D.; Lipp, V.; Veiko, V.; Yakovlev, E.; Rethfeld, B.; Garcia, M. Molecular dynamics study of the short laser pulse ablation: Quality and efficiency in production. Appl. Phys. A 2014, 117, 2133–2141. [Google Scholar] [CrossRef]
- Rämer, A.; Osmani, O.; Rethfeld, B. Laser damage in silicon: Energy absorption, relaxation, and transport. J. Appl. Phys. 2014, 116, 053508. [Google Scholar] [CrossRef] [Green Version]
- Lipp, V.P.; Rethfeld, B.; Garcia, M.E.; Ivanov, D.S. Atomistic-continuum modeling of short laser pulse melting of Si targets. Phys. Rev. B 2014, 90, 245306. [Google Scholar] [CrossRef] [Green Version]
- Rathore, R.; Singhal, H.; Chakera, J. Temporal evolution of photoinduced thermal strain in InSb probed by ultra-short laser produced Cu Kα x-rays. J. Appl. Phys. 2019, 126, 105706. [Google Scholar] [CrossRef]
- Young, J.F.; Van Driel, H. Ambipolar diffusion of high-density electrons and holes in Ge, Si, and GaAs: Many-body effects. Phys. Rev. B 1982, 26, 2147. [Google Scholar] [CrossRef]
- Lietoila, A.; Gibbons, J.F. Computer modeling of the temperature rise and carrier concentration induced in silicon by nanosecond laser pulses. J. Appl. Phys. 1982, 53, 3207–3213. [Google Scholar] [CrossRef]
- Sproul, A.B.; Green, M.A. Improved value for the silicon intrinsic carrier concentration from 275 to 375 K. J. Appl. Phys. 1991, 70, 846–854. [Google Scholar] [CrossRef]
- Wood, R.F.; Giles, G.E. Macroscopic theory of pulsed-laser annealing. I. Thermal transport and melting. Phys. Rev. B 1981, 23, 2923. [Google Scholar] [CrossRef]
- Agassi, D. Phenomenological model for pisosecond-pulse laser annealing of semiconductors. J. Appl. Phys. 1984, 55, 4376–4383. [Google Scholar] [CrossRef]
- Thurmond, C.D. The standard thermodynamic functions for the formation of electrons and holes in Ge, Si, GaAs, and GaP. J. Electrochem. Soc. 1975, 122, 1133–1141. [Google Scholar] [CrossRef]
- Vankemmel, R.; Schoenmaker, W.; De Meyer, K. A unified wide temperature range model for the energy gap, the effective carrier mass and intrinsic concentration in silicon. Solid-State Electron. 1993, 36, 1379–1384. [Google Scholar] [CrossRef]
- Jellison, G.E., Jr.; Modine, F.A. Optical absorption of silicon between 1.6 and 4.7 eV at elevated temperatures. Appl. Phys. Lett. 1982, 41, 180–182. [Google Scholar] [CrossRef]
- Jellison, G.E., Jr.; Modine, F.A. Optical functions of silicon between 1.7 and 4.7 eV at elevated temperatures. Phys. Rev. B 1983, 27, 7466. [Google Scholar] [CrossRef]
- Dziewior, J.; Schmid, W. Auger coefficients for highly doped and highly excited silicon. Appl. Phys. Lett. 1977, 31, 346–348. [Google Scholar] [CrossRef]
- Geist, J.; Gladden, W.K. Transition rate for impact ionization in the approximation of a parabolic band structure. Phys. Rev. B 1983, 27, 4833. [Google Scholar] [CrossRef]
- Meyer, J.R.; Kruer, M.R.; Bartoli, F.J. Optical heating in semiconductors: Laser damage in Ge, Si, InSb, and GaAs. J. Appl. Phys. 1980, 51, 5513–5522. [Google Scholar] [CrossRef]
- Ioffe Physical-Technical Institute. Electronic Archive “New Semiconductor Materials. Characteristics and Properties”; Silicon Properties. Available online: http://www.ioffe.rssi.ru/SVA/NSM/Semicond/Si/ (accessed on 10 November 2019).
- Free Software Foundation. The GNU Scientific Library (gsl-1.15). Available online: https://www.gnu.org/software/gsl (accessed on 10 November 2019).
- Thomas, L. Elliptic Problems in Linear Differential Equations over a Network: Watson Scientific Computing Laboratory; Columbia Univ.: Columbia, NY, USA, 1949. [Google Scholar]
- Bonse, J.; Brzezinka, K.W.; Meixner, A.J. Modifying single-crystalline silicon by femtosecond laser pulses: An analysis by micro Raman spectroscopy, scanning laser microscopy and atomic force microscopy. Appl. Surf. Sci. 2004, 221, 215–230. [Google Scholar] [CrossRef]
- Lipp, V.P. Atomistic-Continuum Modeling of Ultrafast Laser-Induced Melting of Silicon Targets. Ph.D. Thesis, University of Kassel, Kassel, Germany, 2015. [Google Scholar]
- Wang, T.Y.; Lee, Y.M.; Chen, C.C.P. 3D thermal-ADI: An efficient chip-level transient thermal simulator. In Proceedings of the 2003 International Symposium on Physical Design, Monterey, CA, USA, 6–9 April 2003; ACM: New York, NY, USA, 2003; pp. 10–17. [Google Scholar]
- Peaceman, D.W.; Rachford, H.H., Jr. The numerical solution of parabolic and elliptic differential equations. J. Soc. Ind. Appl. Math. 1955, 3, 28–41. [Google Scholar] [CrossRef]
| Parameter Name | Value | Citation |
|---|---|---|
| Initial carrier density | [29] | |
| Initial lattice and carrier temperature | 300 K | |
| Lattice specific heat | ( in K) | [30] |
| Lattice thermal conductivity | , W/(mK) ( in K) | [30] |
| Carrier thermal conductivity | , eV/(s m K) | [31] |
| Indirect band gap | if and 0 otherwise, eV ( in K, n in m) | [32] [33] |
| Interband absorption (taken from 694 laser) | , m | [34] |
| Two-photon absorption | cm/GW | [25] |
| Reflectivity | ( in K) | [35] |
| Auger recombination coefficient | , m/s | [36] |
| Impact ionization coefficient | , s | [37] |
| Free-carrier absorption cross section | , m ( in K) | [38] |
| Electron-phonon relaxation time | , s (n in m) | [31] |
| Electron effective mass | [39] | |
| Hole effective mass | [39] | |
| Mobility of electrons (taken at 1000 K) | m2/V s | [38] |
| Mobility of holes (taken at 1000 K) | m2/V s | [38] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lipp, V.; Rethfeld, B.; Garcia, M.; Ivanov, D. Solving a System of Differential Equations Containing a Diffusion Equation with Nonlinear Terms on the Example of Laser Heating in Silicon. Appl. Sci. 2020, 10, 1853. https://doi.org/10.3390/app10051853
Lipp V, Rethfeld B, Garcia M, Ivanov D. Solving a System of Differential Equations Containing a Diffusion Equation with Nonlinear Terms on the Example of Laser Heating in Silicon. Applied Sciences. 2020; 10(5):1853. https://doi.org/10.3390/app10051853
Chicago/Turabian StyleLipp, Vladimir, Baerbel Rethfeld, Martin Garcia, and Dmitry Ivanov. 2020. "Solving a System of Differential Equations Containing a Diffusion Equation with Nonlinear Terms on the Example of Laser Heating in Silicon" Applied Sciences 10, no. 5: 1853. https://doi.org/10.3390/app10051853





